前言
在实际开发中我们会经常用到寻路算法,例如MMOARPG游戏魔兽中,里面的人物行走为了模仿真实人物行走的体验,会选择最近路线达到目的地,期间会避开高山或者湖水,绕过箱子或者树林,直到走到你所选定的目的地。这种人类理所当然的行为,在计算机中却需要特殊的算法去实现,常用的寻路算法主要有宽度最优搜索、Dijkstra算法、贪心算法、A*搜索算法、B*搜索算法、导航网格算法、JPS算法等,学习这些算法的过程就是不断抽象人类寻路决策的过程。本文主要以一个简单空间寻路为例,对A*算法进行分析实现。
介绍
A*(A-Star)算法是一种静态路网中求解最短路径最有效的直接搜索方法,也是解决许多搜索问题的常用启发式算法,算法中的距离估算值与实际值越接近,最终搜索速度越快。之后涌现了很多预处理算法(如ALT,CH,HL等等),在线查询效率是A*算法的数千甚至上万倍。
问题
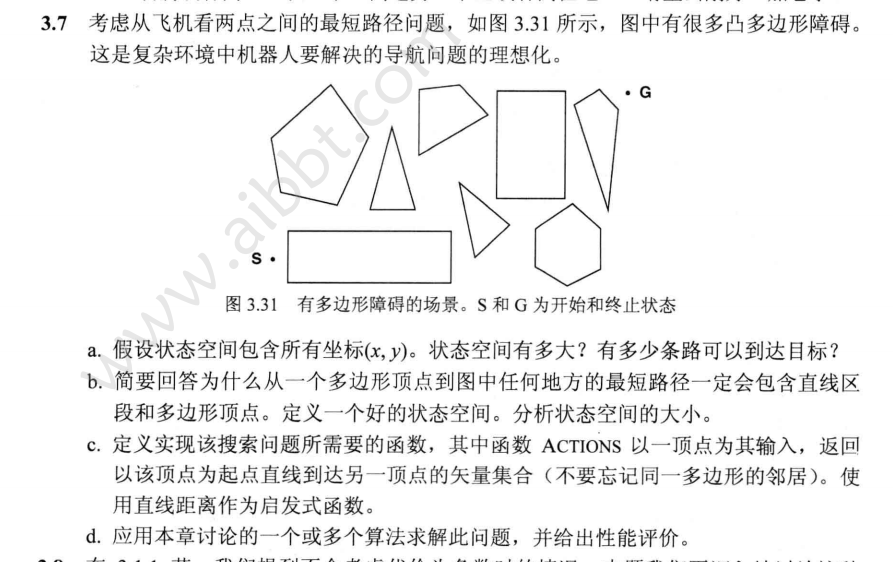
在包含很多凸多边形障碍的空间里,解决从起始点到终点的机器人导航问题。
 问题
问题
步骤
地图预处理
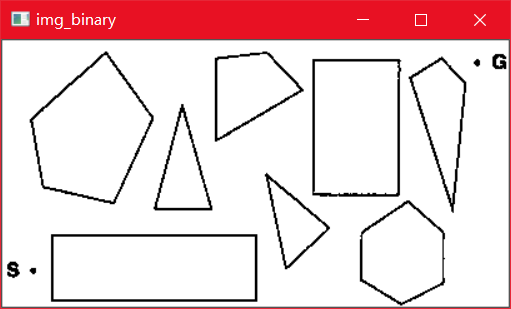
题中寻路地图包含在很多文字之中,且图中还包含logo,这都直接影响了寻路算法的使用,因此需要将图片转程序易处理的数据结构。预处理后地图如下:
 预处理
预处理
算法思想
A*算法为了在获得最短路径的前提下搜索最少节点,通过不断计算当前节点的附近节点F(N)值来判断下次探索的方向,每个节点的值计算方法为:F(N)=G(N)+H(N)。
其中G(N)是从起点到当前节点N的移动消耗(比如低消耗代表平地、高消耗代表沙漠);H(N)代表当前节点到目标节点的预期距离,可以用使用曼哈顿距离、欧氏距离等。当节点间移动消耗G(N)非常小时,G(N)对F(N)的影响也会微乎其微,A*算法就退化为最好优先贪婪算法;当节点间移动消耗G(N)非常大以至于H(N)对F(N)的影响微乎其微时,A*算法就退化为Dijkstra算法。
算法步骤
整个算法流程为:
- 设定两个集合:open集、close集
- 将起始点加入open集,其F值为0(设置父亲节点为空)
- 当open集合非空,则执行以下循环
3.1 在open集中移出一个F值最小的节点作为当前节点,并将其加入close集
3.2 如果当前节点为终点,则退出循环完成任务
3.3 处理当前节点的所有邻居节点,对于每个节点进行以下操作:
- 如果该节点不可达或在close集中则忽略该节点
- 计算该节点的F(N)值,并:如果该节点在open集中且F(N)大于当前F(N),则选择较小F(N)替换;否则将该节点加入open集
- 将该节点的父节点设置为当前节点
- 将该节点加入open集
- 搜索结束如果open集为空,则可能搜索到一条路径;如果open集非空,则必然搜索到一条路径,从终点不断遍历其父节点便是搜索路径。
代码实现
使用Python编写A*算法的核心代码为:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
|
class AStar(object):
'''
@param {*} graph 地图
@param {*} start 开始节点
@param {*} goal 终点
'''
def __init__(self, graph, start, goal):
self.start = start
self.goal = goal
self.graph = graph
# 优先队列储存open集
self.frontier = PriorityQueue()
# 初始化起点
self.frontier.put(start)
'''
@description: 绘出最终路径
'''
def draw_path(self):
path = self.goal
matrix = self.graph.matrix
while path:
matrix[path.x][path.y] = 0
path = path.father
def run(self):
plt.ion()
n = 0
while not self.frontier.empty():
n = n + 1
current = self.frontier.get()
# 是否为终点
if current.equal(self.goal):
self.goal.father = current
self.draw_path()
return True
# 遍历邻居节点
for next in self.graph.neighbors(current):
# 计算移动消耗G
next.g = current.g + self.graph.cost(current, next)
# 计算曼哈顿距离H
next.manhattan(self.goal)
# 如果当前节点未在open集中
if not next.used:
next.used = True
# 将探索过的节点设为阴影,便于观察
self.graph.matrix[next.x][next.y] = 99
# 将当前节点加入open集
self.frontier.put(next)
# 设置该节点的父节点为当前节点
next.father = current
# 没100次更新一次图像
if n % 100 == 0:
plt.clf()
plt.imshow(self.graph.matrix)
plt.pause(0.01)
plt.show()
return False
|
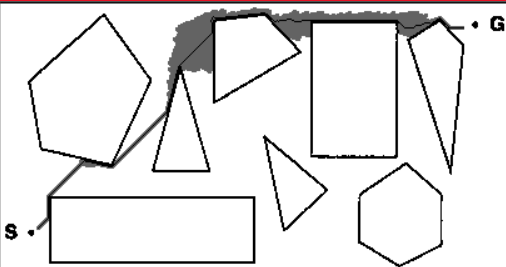
寻路结果如下(其中黑实线是算法得出的最优路径,路径旁边的黑色地带是探索过的节点):
 结果
结果
思考
本例中图像共有406×220像素,即有89320个像素点,也就是状态空间共有89320,可选线路最高有893202约为80亿种,虽然经过了简单的地图优化处理,但直接使用A*算法的效率还是很低。要想进一步提高搜索效率,可以引出另外一条定理:给定平面上一个起始点s和一个目标点g,以及若干多边形障碍物P1, P2, P3 … Pk,由于两点间直线最短,故在所有从s到g的路径中,距离最短的路径的拐点一定在多边形顶点上。基于以上定理,我们可以人工将地图中的多边形顶点进行提取,再用A*算法对提取的顶点进行计算,即可在获得最短路径的同时大大增加了算法的效率。
完整代码
- 数据结构
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
|
from queue import PriorityQueue
import cv2
import math
import matplotlib.pyplot as plt
import fire
class Node(object):
def __init__(self, x=0, y=0, v=0, g=0, h=0):
self.x = x
self.y = y
self.v = v
self.g = g #g值
self.h = h #h值
self.used = False
self.father = None #父节点
'''
@description: 曼哈顿距离
@param {*} endNode 目标节点
'''
def manhattan(self, endNode):
self.h = (abs(endNode.x - self.x) + abs(endNode.y - self.y)) * 10
'''
@description: 欧拉距离
@param {*} self
@param {*} endNode
@return {*}
'''
def euclidean(self, endNode):
self.h = int(math.sqrt(abs(endNode.x - self.x)**2 + abs(endNode.y - self.y)**2)) * 30
'''
@description: 判断other节点与当前节点是否相等
@param {*} other
'''
def equal(self, other):
if self.x == other.x and self.y == other.y:
return True
else:
return False
'''
@description: 函数重载,为了满足PriorityQueue进行排序
@param {*} other
'''
def __lt__(self, other):
if self.h + self.g <= other.h + other.g:
return True
else:
return False
class Graph(object):
'''
@description: 类初始化
@param {*} matrix 地图矩阵
@param {*} maxW 地图宽
@param {*} maxH 地图高
'''
def __init__(self, matrix, maxW, maxH):
self.matrix = matrix
self.maxW = maxW
self.maxH = maxH
self.nodes = []
# 普通二维矩阵转一维坐标矩阵
for i in range(maxH):
for j in range(maxW):
self.nodes.append(Node(i, j, self.matrix[i][j]))
'''
@description: 检查坐标是否合法
@param {*} x
@param {*} y
'''
def checkPosition(self, x, y):
return x > 0 and x < self.maxH and y > 0 and y < self.maxW and self.nodes[x * self.maxW + y].v > 200
'''
@description: 寻找当前节点的邻居节点
@param {Node} node 当前节点
@return {*}
'''
def neighbors(self, node: Node):
ng = []
if self.checkPosition(node.x - 1, node.y):
ng.append(self.nodes[(node.x - 1) * self.maxW + node.y])
if self.checkPosition(node.x + 1, node.y):
ng.append(self.nodes[(node.x + 1) * self.maxW + node.y])
if self.checkPosition(node.x, node.y - 1):
ng.append(self.nodes[node.x * self.maxW + node.y - 1])
if self.checkPosition(node.x, node.y + 1):
ng.append(self.nodes[node.x * self.maxW + node.y + 1])
if self.checkPosition(node.x + 1, node.y + 1):
ng.append(self.nodes[(node.x + 1) * self.maxW + node.y + 1])
if self.checkPosition(node.x + 1, node.y - 1):
ng.append(self.nodes[(node.x + 1) * self.maxW + node.y - 1])
if self.checkPosition(node.x - 1, node.y + 1):
ng.append(self.nodes[(node.x - 1) * self.maxW + node.y + 1])
if self.checkPosition(node.x - 1, node.y - 1):
ng.append(self.nodes[(node.x - 1) * self.maxW + node.y - 1])
return ng
'''
@description: 画出结果路径
'''
def draw(self):
cv2.imshow('result', self.matrix)
cv2.waitKey(0)
cv2.destroyAllWindows()
'''
@description: 计算节点间移动消耗
@param {Node} current
@param {Node} next
@return {*}
'''
def cost(self, current: Node, next: Node):
return 11 if abs(current.x - next.x) + abs(current.y - next.y) > 1 else 10
class AStar(object):
'''
@param {*} graph 地图\n
@param {*} start 开始节点
@param {*} goal 终点
'''
def __init__(self, graph, start, goal):
self.start = start
self.goal = goal
self.graph = graph
# 优先队列储存open集
self.frontier = PriorityQueue()
# 初始化起点
self.frontier.put(start)
'''
@description: 绘出最终路径
'''
def draw_path(self):
path = self.goal
matrix = self.graph.matrix
while path:
matrix[path.x][path.y] = 0
path = path.father
def run(self):
plt.ion()
n = 0
while not self.frontier.empty():
n = n + 1
current = self.frontier.get()
# 是否为终点
if current.equal(self.goal):
self.goal.father = current
self.draw_path()
return True
# 遍历邻居节点
for next in self.graph.neighbors(current):
# 计算移动消耗G
next.g = current.g + self.graph.cost(current, next)
# 计算曼哈顿距离H
next.manhattan(self.goal)
# 如果当前节点未在open集中
if not next.used:
next.used = True
# 将探索过的节点设为阴影,便于观察
self.graph.matrix[next.x][next.y] = 99
# 将当前节点加入open集
self.frontier.put(next)
# 设置该节点的父节点为当前节点
next.father = current
# 没100次更新一次图像
if n % 100 == 0:
plt.clf()
plt.imshow(self.graph.matrix)
plt.pause(0.01)
plt.show()
return False
|
- 主程序
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
|
import cv2
from AStar import Node, AStar, Graph
src_path = "./map.png"
# 读取图片
img_grey = cv2.imread(src_path, cv2.IMREAD_GRAYSCALE)
# 去除水印
img_grey = cv2.threshold(img_grey, 200, 255, cv2.THRESH_BINARY)[1]
# 二值化
img_binary = cv2.threshold(img_grey, 128, 255, cv2.THRESH_BINARY)[1]
img_binary[:][0] = 0
img_binary[:][-1] = 0
img_binary[0][:] = 0
img_binary[-1][:] = 0
start = Node(180, 30)
goal = Node(20, 370)
maxH, maxW = img_binary.shape
graph = Graph(img_binary, maxW, maxH)
astar = AStar(graph, start, goal)
astar.run()
cv2.imshow('result', graph.matrix)
cv2.waitKey(0)
cv2.destroyAllWindows()
|
参考文献